要想在SAT考试中取得155今天，我们特意为大家总结了在SAT考试之前必须熟悉和理解的28个公式，为数学打好基础，助力大家冲刺满分。
　　下面，就一起来看看吧～
　　01几何公式总结
　　以上这些几何公式，你需要做的就是熟悉理解它们，避免在考试时查找公式而浪费时间。
　　以下是12个公式和3个几何定理及解释如下：
　　平面几何公式

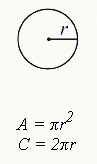
　　► 圆的面积 Area of a Circle
　　A = πr²
　　► 圆的周长Circumference of a Circle
　　C = 2πr 或 C = πd
　　π为常数，在SAT考试中一般以 3.14计算，r为圆的半径，d为圆的直径，长度为半径的两倍。

　　► 矩形面积 Area of a Rectangle
　　A = lw
　　(面积 = 长×宽)

　　► 三角形面积 Area of a Triangle
　　A = ½bh
　　(面积 = ½ ×长×宽)
　　b为三角形一侧底边的长，h为三角形该底边上的高。

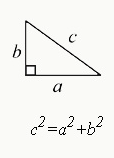
　　► 毕达哥拉斯定理 (勾股定理)
　　The Pythagorean Theorem
　　a²+b²=c²
　　在直角三角形中，两个直角边(a和b)长度的平方之和等于斜边长度(c 三角形最长边)的平方。

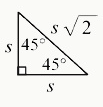
　　► 特殊三角形|等腰直角三角形
　　Properties of Special Right Triangle: Isosceles Triangle
　　边长比：1:1:√2
　　等腰三角形具有两条长度相等的边和与这些边相对的两个相等的角，等腰直角三角形具有一个 90 度角和两个 45 度角。

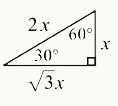
　　► 特殊三角形|30º，60º，90º
　　Properties of Special Right Triangle: 30, 60, 90 Degree Triangle
　　边长比：1:√3: 2
　　含有30º和60º的直角三角形边长比具有以下规律：30º角所对的为最短边，长度为x，则60º角所对边长度为√3x，直角所对边长度为2x。
　　立体几何公式

　　► 长方体体积
　　Volume of a Rectangular Solid
　　V = lwh =Ah
　　(体积 = 长×宽×高 = 底面积×高)

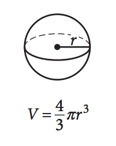
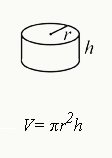
　　► 圆柱体积 Volume of a Cylinder
　　V = πr²h = Ah
　　(体积 = 圆周率×半径²×高 = 底面积×高)

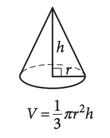
　　► 球体体积 Volume of a Sphere

　　V = 4/3πr³
　　(体积 = 4/3 × 圆周率 × 半径³)
　　► 圆锥体积 Volume of a Cone
　　V = 1/3πr²h = 1/3Ah
　　(体积 = 1/3 × 圆周率 × 半径² × 高
　　= 1/3 × 底面积×高)
　　► 棱锥体积 Volume of a Pyramid
　　V = 1/3lwh = 1/3Ah
　　(体积 =1/3×长×宽×高 = 1/3×底面积×高)
　　► 三大定理 3 Laws
　　圆的度数为360º(the number of degrees in a circle is 360)
　　圆的弧度数为2π(the number of radians in a circle is 2π)
　　三角形内角度数和为180º(the number of degrees in a triangle is 180)
　　02代数和三角函数公式总结
　　坐标系公式Slopes and Graphs
　　► 斜率公式 Slope formula
　　当直线上有两点A(x₁，y₁)，B(x₂，y₂)
　　斜率=(y₂ - y₁)/(x₂ - x₁)
　　► 直线方程 Equation of a line
　　y = mx + b
　　m为直线的斜率(slope)，而b为截距(intercept，直线与y轴的交点坐标)，直线经过零点时，方程写为y = mx。
　　题目可能会给出一个其他形式的方程，问斜率和截距的正负等问题，此时应该将方程改写为规范的直线方程形式再进行思考。
　　► 中点公式* Midpoint formula
　　当直线上有两点A(x₁，y₁)，B(x₂，y₂)
　　两点的中点坐标为
　　( (x₁ + x₂)/2 ，(y₁ + y₂)/2 )
　　► 距离公式* Distance formula
　　当直线上有两点A(x₁，y₁)，B(x₂，y₂)
　　两点间距离为
　　d = √[(x₂ - x₁)²+(y₂ - y₁)²]
　　圆弧公式 Circles
　　► 弧长* Length of an arc
　　L弧 =(2πr)×(圆弧角度数/360º)
　　► 圆弧面积* Area of an arc sector
　　A弧 = (πr²)×(圆弧角度数/360º)
　　代数Algebra
　　► 二次方程 Quadratic equation
　　给定一个多项式，其形式为ax² + bx + c = 0，求解x。
　　代入数字即可求解x
　　(注意需根据±两个算法得出两个x的解)
　　平均数、概率 Averages & Probabilities
　　n表示数据的个数时：
　　► 平均数 Mean/Average
　　A = 数据总和 / n
　　► 平均速度 Average speed
　　S = 总距离 / 总时间
　　求事件A概率时：
　　► 概率 Probability of an outcome
　　P(A) = A事件出现的结果数目 / 所有可能出现的基本结果的总数目
　　三角函数Trigonometry
　　已知三角形各边的长度，求某角的正弦/余弦/正切值。
　　► 正弦 sine： sinA = a / h
　　正弦值 = 角A对边长 / 斜边长
　　Sine equals Opposite over Hypotenuse
　　► 余弦 cosine： cosA = b / h
　　余弦值 = 角A邻边长 / 斜边长
　　Cosine equals Adjacent over Hypotenuse
　　► 正切 tangent： tanA = a / b
　　正切值 = 角A对边长 / 角A邻边长
　　Tangent equals Opposite over Adjacent